FINCAD Analytics Suite 2009 for Excel and FINCAD Analytics Suite 2009 for Developers expand FINCAD's coverage to price and hedge interest rate derivatives consistent with the market smile dynamics by adding pricing functions using the SABR model of stochastic volatility.
To evaluate the lastest version of FINCAD Analytics Suite for free, contact a FINCAD Representative
Overview
The seemingly simple task of pricing and hedging a swaption can become challenging if a volatility smile/skew is present in the market data - defined as a non-constant Black volatility as a function of the exercise rate of the swaption. This is due to the fact that one needs a model consistent with the entire volatility surface.
One of the first successful models to address this need is Dupire's local volatility model [3] which can be self-consistently calibrated to the entire volatility surface. However, as discussed in [4], the dynamic behavior predicted by Dupire's local volatility model is opposite to the behavior empirically observed in interest rate markets. Specifically, Dupire's local volatility model predicts that when the underlying forward rate decreases, the smile shifts to higher prices and when the underlying forward rate increases, that the smile shifts to lower prices.
The Stochastic Alpha Beta Rho (SABR) model is a model of stochastic volatility introduced by Hagan et. al. [4] as an attempt to model the volatility surface and to capture the empirically observed dynamic behavior of the smile.
Besides pricing and hedging the derivatives, another appealing application is to construct the "volatility cube" (vol cube)[1], which is a representation of swaption market data characterized by three parameters: option maturity, swap tenor and exercise rate (or strike). Some parts of the vol cube can be populated by data easily obtained from the market, such as at-the-money (ATM) swaption vols and the Black volatilities for caplets (floorlets) (which can be thought of as one-period swaptions). The rest of the vol cube can be determined by interpolation with the help of the SABR model [1].
The SABR model has gained widespread use due to its tractable pricing, ability to capture both the correct shape of the smile, as well as the correct dynamics of the volatility smile. It also gives practitioners the flexibility to use their intuition regarding market dynamics. For an in depth introduction to the SABR model, consult [4], [5].
FINCAD Analytics Suite 2009 provides functions to value swaptions and interest rate caplets/floorlets along with the functionality to calibrate the SABR model with swaption or caplet/floorlet volatilities.
Pricing Interest Rate Derivatives
Caplets and swaptions are essentially options on the underlying interest rate and forward swap rate, respectively. The SABR model assumes that the underlying rate f follows the stochastic differential equations

Hagan et. al derived the celebrated asymptotic formula for the effective Black volatility in the SABR model [4],
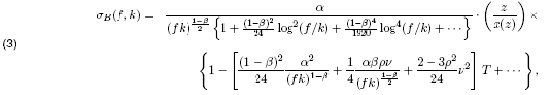

The beauty of the SABR model is that the prices of caplets or swaptions are given by the Black formula with a modified volatility given in Equation (3) as long as the model parameters are in hand. FINCAD Analytics Suite 2009 provides functions to value caplets/floorlets and swaptions in the SABR model:
aaCaplet_SABR calculates the price and risk statistics of a caplet/floorlet.
aaSwaption_SABR calculates the fair strike and risk statistics of a swaption.
aaSwaption_SABR_fs calculates the fair strike and risk statistics of a swaption and allows free-style user inputs.
Calibration
With a suitable set of SABR parameters in hand, pricing simply reduces to a calculation of the effective Black volatility, via Equation (3), to use in the Black formula. The bulk of the effort, therefore, comes down to choosing the "best" set of SABR parameters. The SABR parameters in Equation (1) can be determined by calibration to caplet/floorlet or swaption market data. The procedure will be slightly different for swaption calibration since ATM vol is more important than non-ATM vols.
It is empirically seen that the two parameters ρ and β have similar effects on the vol smile in that they both control the amount of skewness. Mathematically, (sometimes referred to as the "skewness" parameter) is a constant elasticity of variance (CEV) exponent (see [2]). β = 1 corresponds to a stochastic lognormal model and β = 0 corresponds to a stochastic normal model.
There are two methods used for determining β, both of which stem from the analytical form of the ATM vols in the SABR model, calculated by setting the strike rate k in Equation (3) to equal the forward rate f
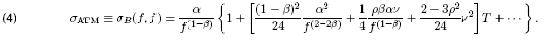
The skewness parameter can be determined by performing linear regression on the log-log plot of historical par swap rates versus ATM vols [4] given by Equation (4).
Alternatively, β can be chosen by the practitioner by appealing to their market intuition. This may seem like an ad-hoc method to choose β, however by investigating Equation (4), specifically the behavior of the ATM vol as a function of β

This approximate equation describes the so-called "backbone", defined as the curve followed by the ATM vol as a function of the par swap rate. As the par swap rate changes, this curve represents how these changes affect the ATM vol. Notice that in the stochastic lognormal model, where β = 1 the backbone is flat. Financially this corresponds to a constant level of overall forward swap rates as the par swap rate changes. Some practitioners use this model since it represents a common model used throughout finance and they believe that the flat backbone "best represents their market" [4]. Nevertheless, the parameter β is usually chosen exogenously, and not via calibration.
Calibration of SABR parameters to swaption data proceed differently than the two other instrument classes (options and caplets/floorlets) in that when calibrating to swaptions, the parameter α is not determined by calibration, instead it is determined by the Equation (4). Given αATM, β, ρ and ν, Equation (4) can be inverted to give a cubic equation whose roots yield the value of α, meaning that the parameter α is chosen so that the ATM vols seen in the market are reproduced exactly. This is not done for caplets because caplets ATM data is not a widely quoted number - it may or may not exist in the marketplace. Swaption market data, on the other hand, is typically only quoted as ATM vols, so this must be taken into account during calibration.
FINCAD Analytics Suite 2009 provides functions to calibrate the SABR model to caplets/floorlets or swaptions data:
aaCalibrateCaplets_SABR calibrates the SABR model to caplet/floorlets.
aaCalibrateSwaptions_SABR calibrates the SABR model to swaptions.
Volatility Cube
As mentioned before, vol cube is a representation of swaption market data characterized by three parameters: option maturity, swap tenor and exercise rate (or strike). Market data can be used to directly populate two of the "faces" of the vol cube as follows.
First, the at-the-money (ATM) swaption vols can populate the ATM slice (defined by the condition that the exercise rate is the par swap rate).
Second, rate caps and floors can be used to populate the slice containing the smallest swap tenor. To achieve this, the caps (floors) must first be stripped to produce the Black volatility of the constituent caplets (floorlets) (this step can be achieved by using the FINCAD function aaVol_Crv2_Rcap_BL). The resulting series of caplets/floorlets can be thought of as one-period swaptions with a swap tenor equal to the frequency of the cap/floor.
With one more piece of information, we can construct the entire vol cube. In order to be able to use the function aaCalibrateSwaptions_SABR, we need more than just the ATM swaption market quotes. According to [1] there are two methods to determine non-ATM swaption vols. The method advocated by FINCAD is to apply the same smile shape as seen in the caplet data to the swaption vols. Numerically, this means that one calculates the difference between the furthest out-of-the-money OTM) and in-the-money (ITM) caplet vols and applies this difference to the swaption ATM vol to produce the corresponding non-ATM vols. For instance, suppose the par swap rate is 6%, and we see the following market caplet vols.
| Strike | Black Vol |
| 2% | 21.5% |
| 4% | 16.7% |
| 6% | 14.4% |
| 8% | 16.1% |
| 10% | 15.0% |
The skew can be characterized by two numbers δ2% ≡ α2% - αATM = 7.1% and δ10% ≡ α10% - αATM = 0.6%. To produce the swaption data, simply apply these skewness shifts to the swaption data. A non-ATM swaption vol is approximated as α = αATM + δi. In the above scenario, with a 10Yx10Y swaption with an ATM vol of 11%, the two data points to use in the calibration are α2% = 11% + δ2% = 18.1% and α10% = 11% + δ10% = 11.6%. According to [1] this procedure is "not just 'parallel shifting' the caplet smile to longer swap tenors, but we are, on the contrary, calculating the implied cap smile in the surface instead". The FINCAD function aaCalibrateSwaptions_SABR will fix α by requiring the calibration to reproduce the ATM volatility exactly, and the other parameters by the usual minimization procedure. This method can therefore be used to interpolate in all the dimensions of the vol cube.
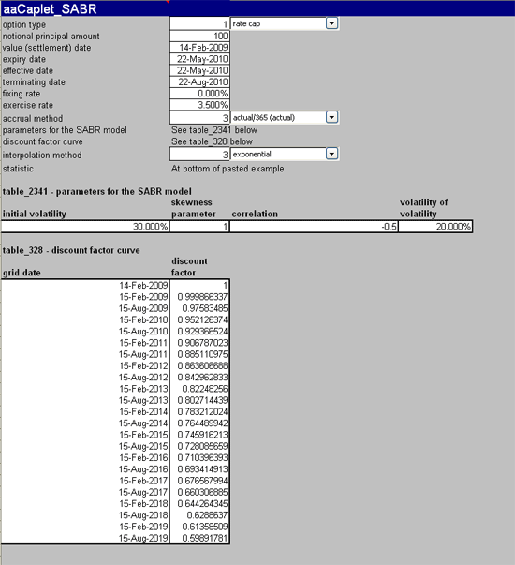
Figure 1: Screen shot of the inputs to aaCaplet_SABR for the calculations
Example: Pricing a Caplet
In this example, we calculate the fair value and all risk statistics for a caplet using the SABR model. We use the FINCAD function aaCaplet_SABR for our calculations. Figure 1 shows the inputs for this function.
Given the inputs in Figure 1, we find the fair value of the caplet is 0:361, which was calculated with the function aaCaplet_SABR. The other risk statistics are shown in Figure 2.

Figure 2: Screen shot of the outputs from aaCaplet_SABR
Summary
FINCAD Analytics Suite 2009 provides functions to compute prices and all risk statistics for caplets/floorlets and swaptions using the SABR model. It also provides a function to calibrate the SABR model to market caplets/floorlets or swaptions data, which enable users to construct the volatility cube.
To evaluate the lastest version of FINCAD Analytics Suite for free, contact a FINCAD Representative
References
[1] Banking, SEB Merchant (2008), SEB's VolCube, Research Paper.
[2]Cox, J. (1975), Notes on Option Pricing 1: Constant Elasticity of Variance Diffusions, Working Paper, Stanford University.
[3]Dupire, B. (1994), Pricing with a Smile, Risk, 7(1): pp. 18-20.
[4] Hagan, Patrick S., Kumar, D., Lesniewski, A. S., and Woodward, D. E. (September 2002), Managing smile risk, Wilmott, pp. 84-108.
[5] Option Pricing with the SABR Model of Stochastic Volatility (2008), Math Reference Document, FINCAD.
