In recent years, trading mortgage-backed securities (MBS) has gained increased popularity. This trend is largely due to financial institutions embracing more sophisticated investment strategies, involving new and diverse asset classes, as they work to boost investment returns.
The good news is that today MBS are a much safer investment type than they were in the direct aftermath of the credit crisis. In fact, currently U.S. mortgage holders are performing well in terms of keeping up with their loan payments, and home prices have crept up steadily over the last couple of years.
But of course trading MBS is nothing new. In actuality these securities have been around since the early 1990’s. However, over the years there have been changes made to how we model MBS. The below timeline gives the historical evolution of MBS behavioral modeling from its beginnings through to current times.
- Early 1990’s: During this time, static vectors, including the Public Securities Association (PSA Curve), were used by collateral type for credit and prepayment modeling.
- Late 1990’s: A transition to dynamic pool level models meant we looked at variables such as the pool’s weighted average coupon and its seasoning. The most important part of this transition was a dynamic interest rate effect so that as the interest rate shifted, the model tended to respond in a dynamic fashion. Meanwhile, in the late 90’s market practitioners (other than the two government-sponsored enterprises (GSEs) were still using static vectors for credit.
- Early 2000’s: The evolution of loan level prepayment models was primarily driven by better disclosure and improved computing power, providing much greater granularity, while also requiring significantly more processing time for analytical systems.
- 2005-2009: Heading into the credit crisis, we saw the emergence of dynamic credit models in the non-agency space.
- 2013: Once Fannie Mae and Freddie Mac started securitizing credit-sensitive bonds referencing their collateral, market practitioners received the data to begin modeling defaults initially, and then later, severities. This led to the use of dynamic credit models in the agency space as well.
For those looking to begin trading MBS prepayments and defaults, there are a couple of choices available for modeling them. One is to model the constant prepayment rate (CPR) for prepayments, and for defaults, model the constant default rate (CDR). Another option is to model each of the individual transitions leading up to prepayment or default.
Instead of looking at the individual transitions that lead to default, CPR/CDR models are more focused on the end event of default, which could take up to a year or two to occur. Image 1.0 shows an example of a model, actual ending balance and CDR for a CPR/CDR model.
Image 1.0: CPR/ CDR
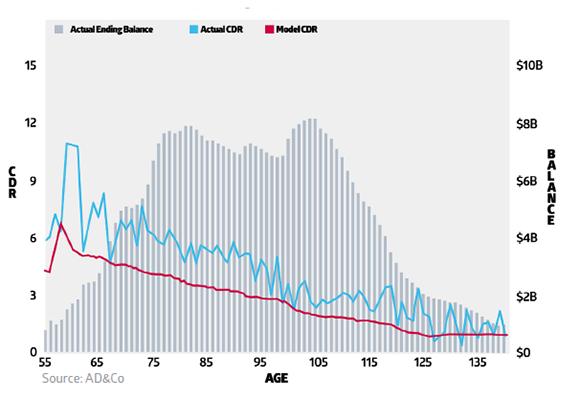The area on the right shows an individual transition rate, which here is an example of a current loan transitioning to delinquent, or becoming a defaulted loan.
Loans typically progress from being current to being 30, 60 or 90 days delinquent. Depending on how long the default process goes, a given loan could increase to 150-180 days delinquent. Thus, one of the early choices that a modeler needs to make is determining how many of these timing transitions to actually use. If you select to use a more granular set of transitions, you will often find there is less data and more noise to deal with between the individual transitions you need to estimate.
On the other hand, a certain degree of granularity is needed to build a good model. Depending on the application, the answer may be different. For example, in the world of servicing, it is quite important to have a finer granularity distinction between states of delinquency. For the purpose of modeling the following example, I have used three primary buckets.
Image 2.0 depicts that current loans are 0-1 month, delinquent loans are 2-5 months and seriously delinquent loans are 6 months and above. There are also a couple of terminated states, including voluntary terminations, which are essentially prepayments or short-sales, and involuntary terminations, which are defaults. Post default there is an additional model that is required to measure the probability of recovery or loss, including how much that loss may be.
Image 2.0: Prepay and Default - Concise Transitions
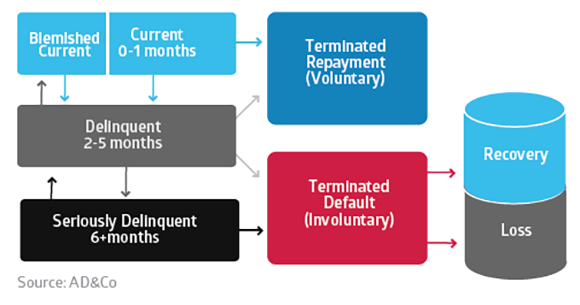
Referring again to image 2.0, each arrow represents individual transitions that need to be modeled. Depicted here are transitions from:
- current to delinquent
- delinquent back to current
- delinquent to seriously delinquent
- seriously delinquent to somewhat delinquent
- current to terminated, or the prepayment termination
- delinquent to terminated, which could be a short-sale or a voluntary terminated state
Upon determining your transitions, you will then need to consider what set of dynamic and static variables you need for your model. Static variables of a given loan do not change over time. These include the type of loan (issuer, original term, etc.), the loan-to-value (LTV) ratio, and the loan state (judicial foreclosure, foreclosure timelines, etc). Conversely, dynamic variables fluctuate either over time or depending on changes in environmental variables. These could include changes in house prices, how seasoned a loan is, interest rates or the economy.
Once your static and dynamic variables are in place, turn your attention to how to model those variables and the predictor variables using a functional form. There are a few different standard functional form choices available. Two that are often used are the standard normal probability distribution and the logistic probability distribution in a regression framework. The advantage of standard textbook functional forms is that estimation is relatively simple. The parameters of such models can be easily estimated. The disadvantage is that they are not as effective for use with complex interactions.
For these complex interactions, market practitioners will often use the piecewise linear approach, particularly for S-shaped curves that relate interest rate incentives to prepayment behavior, or that relate current loan-to-value ratios to default incentives. The reasoning is that often in practice when you look at data, the empirical relationships mainly show knot points and slope changes that are not necessarily as well modeled by an S-shaped curve. However, the trade-off of using a piecewise linear approach is that it requires the use of estimation software that you either need to build internally or obtain from a specialized provider.
Because MBS are a unique investment type, I would encourage you to consider investing in an analytics system built on a generic framework that can help you consistently handle all of your trades and portfolios, including MBS. The system should be flexible, enabling you to change your modeling approach as needed, without reengineering, and give you the tools necessary to reduce model risk.
For more information and detailed examples on MBS modeling, download the newly released eBook: Best Practices in MBS Valuation and Risk.
